モンティホール問題の説明「直観は間違う！陥りやすい思考のワナ」

どうも、Joy@そろ勉です。
モンティホール問題の分かりやすい解説を教えてもらったのでご紹介します。別に難しくないです。ちょっと賢くなった気になれますので、是非一読して、誰かに説明してあげてください。

モンティ・ホール問題とは？

「モンティ・ホール問題」とは、ベイズ定理における事後確率の例題として出てくる問題です。また、「直観で正しいと思える解答と、論理的に正しい解答が異なる問題」の例としてよく取り上げられます。

「なんか小難しそうだなー、オイ！」

と思われたかもしれませんが、とても簡単な話なので、大丈夫です。話のネタにもなりますし、ちょっと賢くなった感じがしますよ。（実際、この考え方は日常生活で使えます。）

「モンティ・ホール問題」の名前の由来は、アメリカの有名なクイズ番組の司会者・モンティ・ホールさん（みのもんたさんをイメージしてください）からきています。

まず、モンティ・ホール問題が、どんな内容か説明します。初見の方は是非、一緒に考えてみてくださいね。

■■問題■■

あなたは、あるテレビのクイズ番組で優勝しました。

優勝の景品はハワイ旅行なのですが、条件があります。
それは、３つのドアの中から１つを選んで、その内１つがハワイ旅行で、残り２つのドアの後ろにはヤギが入っています。

つまり、１個だけが当たりで「ハワイ旅行」です。他の２つは「ハズレ」です。

Ａ・Ｂ・Ｃの３つのドアの中から、あなたは「Ａ」を選びました。

すると司会者（モンティさん）は、残りのドアの内の「Ｃ」のドアを開けて、ヤギが入っているのを見せてくれました。司会者はどのドアが当たりか分かっているからです。

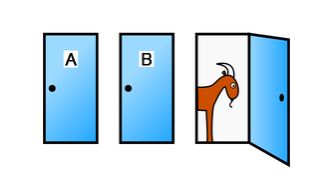
そして、この時点であなたにオプションが与えられました、

「今なら、AからBに変えてもいいですよ！」
「変えますか？変えませんか？」

あなたは迷います。

「ファイナル・アンサー？」

司会者がプレッシャーをかけてきます。

さて、あなたは、選択を変更しますか？しませんか？

・・・

・・

・

いかがでしょうか？
考えてみましたか？
自分の考えを決めてから続きを読んでくださいね。

モンティ・ホール問題の解答

大丈夫でしょうか？

では、解答です。

これは、「事前確率」と「事後確率」を考える問題なのです。
事前確立は、それぞれ３分の１です。
つまり、はじめの段階でハワイ旅行が当たる確率は、どのドアを選んでも３分の１です。

あなたは、Ａを選びました。
このときあなたが当たりを引く確率は、１/３です。あなたが超能力者なら話は別かもしれませんが、通常は１/３ですよね。
そして、ＢとＣのいずれかに当たりが入っている確率は、１－１/３。
つまり、２/３です。これが「事前確率」になります。

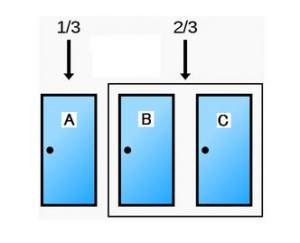
ここまでは大丈夫ですよね？

ここで、司会者モンティさんが、「Ｃ」を開けてハズレだと教えてくれました。

すると、この段階での確率はどう変わるでしょうか？（事後確率）

Ａ⇒1/3
Ｂ・Ｃ⇒2/3

だったところ、Ｃを消してくれた訳ですから、
事後確率は、

Ａ⇒1/3
Ｂ・Ｃ⇒2/3

になります。

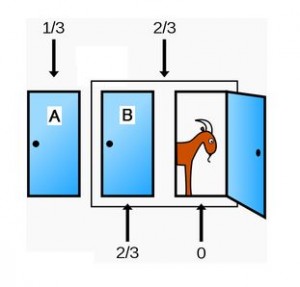
では、もう一度質問します。
ＡとＢのどちらを選択するのが賢いでしょうか？

これはもう明らかですよね？

Aが当たりの確率は３分の１ですが、Bが当たりの確率は３分の２なので、当然Bに変更するのが賢い選択になるわけです。

大丈夫でしょうか。
この説明で納得できたんじゃないかと思います。

是非、家族や友達に問題を出して説明してあげてください。ちょっと賢くみられるかもしれませんよ。また、人に説明することで完全に自分のものになります。

モンティ・ホール問題が出てくる映画作品

この問題、ロバート・ルケティック監督の『ラスベガスをぶっつぶせ』という映画に中でも出てきます。マサチューセッツ工科大学に通う主人公が、ケヴィン・スペイシー演じる教授に、この問題を出されて正解を即答します。これがきっかけでギャンブルの才能を認められ、ラスベガスのブラックジャックで一山当てるチームに勧誘されるのです。

⇒ Amazonで詳細を見る。
⇒ 楽天ブックスで詳細を見る。